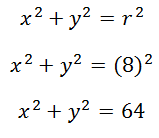Ecuación de la elipse con centro (h,k)

FÓRMULA.

VIDEO EXPLICATIVO.

EJEMPLO. Encontrar los focos y los vértices de la elipse cuya ecuación es 

Solución.

Gráfica.

EJERCICIOS PARA RESOLVER.

En los problemas del 1 al 3, encuentre el centro los focos y los vértices de la elipse dada.

1. 

2. 

3. 

En los problemas 4 y 5, encuentra una ecuación de la elipse que cumpla las condiciones dadas.

4. Centro (-2,2), un foco en (-2,4), a =6.

5. Extremos del eje mayor en (4,2) y (4,13), un foco en (4,4).

Ecuación de la elipse con centro en el orígen.

DEMOSTRACIÓN.



VIDEO EXPLICATIVO.

EJEMPLO. Encontrar los vértices y los focos de la elipse cuya ecuación es


Solución.

Gráfica.

EJERCICIOS PARA RESOLVER.

1. Hallar la ecuación de la elipse con vértices (0,+-2) y focos en (0,+-1)
2. Hallar el centro, los focos y los vértices de la elipse cuya ecuación es

3.  Hallar la ecuación de la elipse con V1(0,8) y V2(0,-8) ; y  F1(0,2) y F2(0,-2).

4.  Hallar el centro, los focos y los vértices de la elipse cuya ecuación es 

5. Un foco en (2,0), centro en (0,0) y b =3.

ELIPSE.

LA ELIPSE.

Definición.  Es el conjunto de todos los puntos P en un plan tal que la suma de las distancias entre P y dos puntos fijos F1 Y F2 es constante. Los dos puntos fijos F1 Y F2 se llaman focos. El punto medio del segmento de recta que une los focos se llama centro.

ELEMENTOS DE UNA ELIPSE.

Ecuación de la circunferencia con centro (h, k)

                                                                                                                                                                                                                                                                                                                                                                                      ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO (H,K)

FORMA CANÓNICA.

FORMA GENERAL.

FÓRMULAS PARA HALLAR LA ECUACIÓN DE LA CIRCUNFERENCIA.

VÍDEO EXPLICATIVO.

EJEMPLO. Halle la ecuación de la circunferencia con centro en C(4,3) que pasa por el punto (1,4)

Solución.

Gráfica.

EJERCICIOS PARA RESOLVER.

1. Halle el centro y el radio de la circunferencia cuya ecuación es : 

2. Hallar la ecuación de la circunferencia con centro (-9,-4) y radio de 3/2.

3. Hallar la ecuación de la circunferencia con centro en (5,6) y pasa por el punto (-3,7).

4, Halle el centro y el radio de la circunferencia cuya ecuación es 

5. Halle la ecuación de una circunferencia con centro en (-3,2) y radio 6.

Ecuación de la circunferencia con centro en el orígen.

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO EN EL ORÍGEN. 

Para hallar el radio, utilizamos la fórmula de la distancia:

VIDEO EXPLICATIVO.

EJEMPLO.

1. Hallar la ecuación de la circunferencia con centro en el orígen y radio de 8 cm.

SOLUCIÓN.

  

Gráfica.

EJERCICIOS PARA RESOLVER.

1. Halle la ecuación de la recta con centro en el orígen y un radio de 15 cm.

2. Halle la ecuación de la recta con centro en (0,0) y pasa por el punto (-5,3).

3. Determine los puntos por donde pasa la circunferencia 

4. Halle la ecuación de la recta con centro en el orígen y un radio de 9cm.

5. Halle la ecuación de la recta con centro en (0,0) y pasa por el punto (-3,-2).

CIRCUNFERENCIA.

DEFINICION. Es un lugar geométrico de un conjunto de infinitos puntos que equidistan de un punto situado en el centro.

ELEMENTOS DE UNA CIRCUNFERENCIA.

PROPIEDADES BÁSICAS DE LA CIRCUNFERENCIA.

1. Radio trazado al punto de tangencia es perpendicular a la recta tangente.

2. Radio o diámetro perpendicular a una cuerda la biseca (divide en dos segmentos congruentes).

3. Cuerdas paralelas determinan arcos congruentes entre las paralelas.

4. A cuerdas congruentes en una misma circunferencia les corresponden arcos congruentes.

POSICIONES RELATIVAS DE DOS CIRCUNFERENCIAS.

-Circunferencias concéntricas. Tienen el mismo centro.

-Circunferencias exteriores. No tienen ningún punto en común.

. Circunferencias Tangente exteriores. Tienen un punto en común que es el de la tangente.

-Circunferencias tangentes interiores. Tienen un punto en común que es la de Tangencia.

. Circunferencias Secantes. Tienen dos puntos comunes que son las intersecciones.

- Circunferencias Ortogonales. Los radios son perpendiculares en el punto de intersección.

- Circunferencias interiores. No tienen puntos comunes.

TEOREMA DE PONCELET.

En todo triángulo rectángulo la suma de longitudes de los catetos es igual a la longitud de la hipotenusa más el doble del inradio.

TEOREMA DE PITOT.

En todo cuadrilátero circunscrito a una circunferencia, se cumples que la suma de longitudes de los lados opuestos son iguales.

ÁNGULOS DE LA CIRCUNFERENCIA.

- Medida del ángulo central. Es igual a la medida del arco que se opone.

. Medida del ángulo interior. Es igual a la semisuma de las medidas de los arcos opuestos.

- Medida del ángulo inscrito. Es la mitad de la medida del arco opuesto

- Medida del ángulo semi-inscrito. Es igual a la medida del arco opuesto. 

- Medida del ángulo ex-inscrito. Es igual a la metad de la medida del arco ABC. 

ANGULOS EXTERIORES. Son tres casos:

* Medida del ángulo formado por dos rectas tangentes.  Es igual a la semidiferencia de las medidas de los arcos opuestos.

* Medida del ángulo formados por dos rectas secantes.  Es igual a la semi-diferencia de los arcos opuestos.

*Medida del ángulo formado por ua recta tangente y otra secante : Es igual a la semidiferencia de los arcos opuestos.